TRANSFORMATIONS

The 'a' value tells us if the graph is vertically stretched or compressed. It also tells us if our parabola is facing up or down.

If the a value is is negative that shows us the parabola is opening down. If our a value is positive, the graph will open up. The graph can also be vertically stretched or compressed according to the a value. So, if the value is less than one (for example, 0.25x) our graph is vertically compressed. If the value is more than one, the graph is vertically stretched.

EXAMPLES:

y=-3x² y= 0.5x²

THE GRAPH IS y=-3x², THEREFORE THE EQUATION IS NEGATIVE SO THE GRAPH WILL OPEN DOWN. THE GRAPH IS ALSO VERITCALLY STRETCHED BY A FACTOR OF -3.

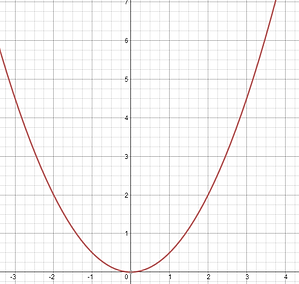
THE GRAPH IS y= 0.5x², THEREFORE THE EQUATION IS POSITIVE SO THE GRAPH IS OPENING UP. THE GRAPH IS VERTICALLY COMPRESSED BY A FACTOR OF 0.5

The 'h' value tells us if the parabola translates to the right or left by h units. If the 'h' value is negative that means the parabola is translated to the right and if the 'h' value is positive that means the parabola moves to the left by h units.

EXAMPLES:

THE EQUATION IS y= (x-7)², THEREFORE THE PARABOLA IS TRANSLATED RIGHT BY 7 UNITS.

THE EQUATION IS y= (x+8)², THEREFORE THE PARABOLA IS TRANSLATED LEFT BY 8 UNITS.

The 'k' value tells us if the parabola is translated up or down by k units. If the 'k' value is positive that means the parabola is translated up and if the 'k' value is negative that means the parabola is translated down.

EXAMPLES:

THE EQUATION IS y= (x² + 6), THEREFORE THE PARABOLA IS TRANSLATED 6 UNITS UP.

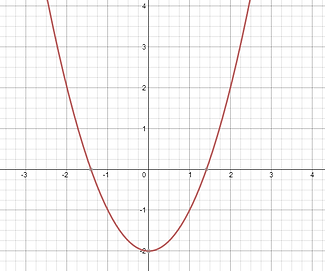
THE EQUATION IS y= (x² -2), THEREFORE THE PARABOLA IS TRANSLATED 2 UNITS DOWN.